Python曲线拟合

2020-04-12 约 1188 字预计阅读 3 分钟次阅读

Python曲线拟合

本文环境：

OS：Ubuntu 18.04.4 LTS
Python版本：3.6.9

曲线拟合

现在我们有一组数据，表达的含义是在不同的时间点的充值金额，反映在坐标上就是一系列的散点，我们希望选择适当的曲线类型（如y = a*x^2 + b）“最佳”地逼近或拟合已知数据，这便是曲线拟合（curve fitting）。当然，变量间未必都是线性关系，我们可能会用到指数函数、对数函数、幂函数等。

Python拟合库

Python的SciPy库是一个用于数学、科学、工程领域的常用软件包，可以处理插值、积分、优化、图像处理、常微分方程数值解的求解、信号处理等问题。SciPy是基于NumPy，所以你也需要安装NumPy，另外用了Matplotlib库来绘制图表，所以也需要安装Matplotlib。（Python在科学计算领域，numpy、Scipy、Matplotlib是非常受欢迎的三个库）

使用案例

首先安装所需依赖（pip使用豆瓣镜像）

1
pip  install  -i  https://pypi.doubanio.com/simple/  numpy scipy matplotlib

多项式拟合

第一种是进行多项式拟合，数学上可以证明，任意函数都可以表示为多项式形式。用的函数是numpy的polyfit函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
import matplotlib.pyplot as plt

# 定义x、y散点坐标
x = [10, 20, 30, 40, 50, 60, 70, 80]
y = [174, 236, 305, 334, 349, 351, 342, 323]

# 转化为numpy的数组
x = np.array(x)
y = np.array(y)

# 这里的3表示最高幂，也就是函数形式为y = a* x^3 + b * x^2 + c * x + d
parameter = np.polyfit(x, y, 3)
print('函数系数为:\n', parameter)

func1 = np.poly1d(parameter)
print('函数为 :\n', func1)

# 也可使用newY=np.polyval(func1, x)
newY = func1(x)  # 拟合y值

# 绘图
plot1 = plt.plot(x, y, 's', label='original values')
plot2 = plt.plot(x, newY, 'r', label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4)  # 指定legend的位置右下角
plt.title('polyfitting')
plt.show()

拟合结果: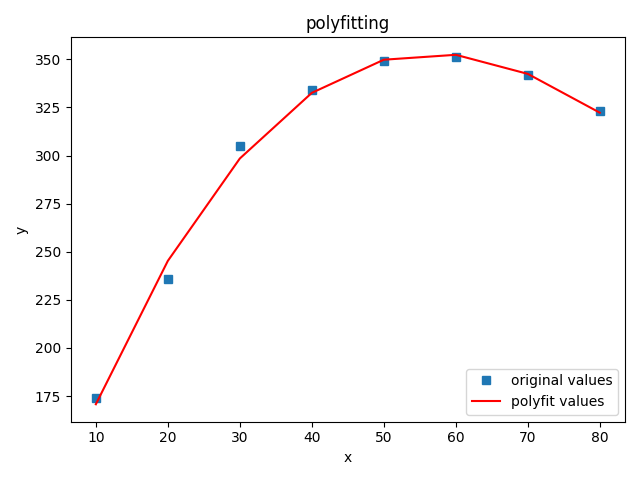

给定函数形式拟合

scipy模块的子模块optimize中提供了一个专门用于曲线拟合的函数curve_fit()
下面通过示例来说明一下如何使用curve_fit()进行直线和曲线的拟合与绘制。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
 
#直线方程函数
def f_1(x, A, B):
    return A*x + B
 
#二次曲线方程
def f_2(x, A, B, C):
    return A*x*x + B*x + C
 
#三次曲线方程
def f_3(x, A, B, C, D):
    return A*x*x*x + B*x*x + C*x + D
 
def plot_test():
 
    plt.figure()
 
    #拟合点
    x0 = [1, 2, 3, 4, 5]
    y0 = [1, 3, 8, 18, 36]
 
    #绘制散点
    plt.scatter(x0[:], y0[:], 25, "red")
 
    #直线拟合与绘制
    A1, B1 = optimize.curve_fit(f_1, x0, y0)[0]
    x1 = np.arange(0, 6, 0.01)
    y1 = A1*x1 + B1
    plt.plot(x1, y1, "blue")
 
    #二次曲线拟合与绘制
    A2, B2, C2 = optimize.curve_fit(f_2, x0, y0)[0]
    x2 = np.arange(0, 6, 0.01)
    y2 = A2*x2*x2 + B2*x2 + C2 
    plt.plot(x2, y2, "green")
 
    #三次曲线拟合与绘制
    A3, B3, C3, D3= optimize.curve_fit(f_3, x0, y0)[0]
    x3 = np.arange(0, 6, 0.01)
    y3 = A3*x3*x3*x3 + B3*x3*x3 + C3*x3 + D3 
    plt.plot(x3, y3, "purple")
 
    plt.title("test")
    plt.xlabel('x')
    plt.ylabel('y')
 
    plt.show()
 
    return

当然，curve_fit()函数不仅可以用于直线、二次曲线、三次曲线的拟合和绘制，仿照代码中的形式，可以适用于任意形式的曲线的拟合和绘制，只要定义好合适的曲线方程即可。

参考：

目录

Python曲线拟合

Python曲线拟合

曲线拟合

Python拟合库

使用案例

多项式拟合

给定函数形式拟合