本文环境：

• OS：Ubuntu 18.04.3 LTS
• Qt版本：5.14.1
• Qt Creator版本：4.10.1

布局器概览

我们以下图的 Qt 设计师界面来说明布局功能，QtCreator 设计模式的布局功能与 Qt 设计师是一样的。

本文环境：

• OS：Ubuntu 18.04.3 LTS
• Qt版本：5.14.1
• Qt Creator版本：4.10.1

Qt安装

首先，我们得明白一些概念。
Qt是一个C++库，或者说是开发框架，里面集成了一些库函数，提高开发效率。
Qt Creator是Qt集成开发环境，你可以在这里编写，编译，运行你的程序。所以最开始写Qt只安装Qt Creator这个是不行的，因为还没有相关的Qt库呢，但是新版的Qt Creator（5.9开始）已经集成了Qt了，所以入门就方便很多了。
关于Qt下载，大家可以打开这里的链接，里面有各版本Qt（Qt和Qt Creator的集成包），操作简单，最新版本是5.14。

Veth

Veth缩写是Virtual ETHernet。veth设备是在linux内核中是成对出现（所以也叫veth-pair），两个设备彼此相连，一个设备从协议栈读取数据后，会将数据发送到另一个设备上去。这个设备其实是专门为container所建的，作用就是把一个network namespace发出的数据包转发到另一个namespace（通常就是宿主机）。

我们都知道，Linux实际是通过网络设备去操作和使用网卡的，系统安装了一个网卡之后会为其生成一个网络设备实例，比如eth0（或者叫enp7s0，不同发行版默认网卡命名规则不同）。随着网络虚拟化技术的发展，Linux支持创建出虚拟化的设备，可以通过虚拟化设备的组合实现多种多样的功能和网络拓扑。
常见的虚拟化设备有tun/tap、Veth、Bridge、802.1q VLAN device。

Kubernetes，简称 k8s（k，8 个字符，s——明白了？）或者 “kube”，是一个开源的 Linux 容器自动化运维平台，它消除了容器化应用程序在部署、伸缩时涉及到的许多手动操作。换句话说，你可以将多台主机组合成集群来运行 Linux 容器，而 Kubernetes 可以帮助你简单高效地管理那些集群。构成这些集群的主机还可以跨越公有云、私有云以及混合云。

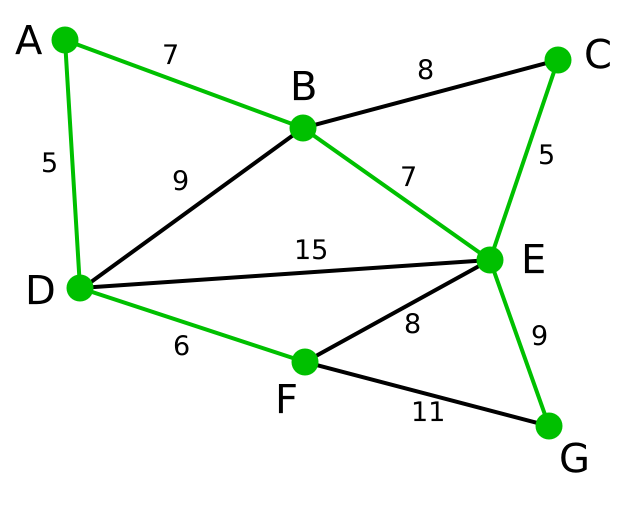
解决最小生成树（Minimum spanning tree）问题的算法，书上介绍了两个：Prime算法和Kruskal算法。

Prim算法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <stdio.h>
#include "graph.h"

extern void DispMat1(MGraph);
void Prim(MGraph g, int v)
{
    int lowcost[MAXV], min, n = g.n;
    int closest[MAXV], i, j, k;
    for (i = 0; i < n; i++)
    {
        lowcost[i] = g.edges[v][i];
        closest[i] = v;
    }
    for (i = 1; i < n; i++)   // 找出n - 1个顶点
    {
        min = INF;
        for (j = 0; j < n; j++)
        {
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;
            }
        }
        printf("    边（%d， %d）权为：%d\n", closest[k], k, min);
        lowcost[k] = 0;      // 标记k已经加入U
        for (j = 0; j < n; j++)
        {
            if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])
            {
                lowcost[j] = g.edges[k][j];
                lowcost[j] = k;
            }
        }
    }
}

Kruskal算法

实现克鲁斯卡尔算法的关键是判断选取的边是否与生成树中已保留的边形成回路，这可以通过判断边的两个顶点所在的连通分量来解决（给顶点所在连通分量编号）。