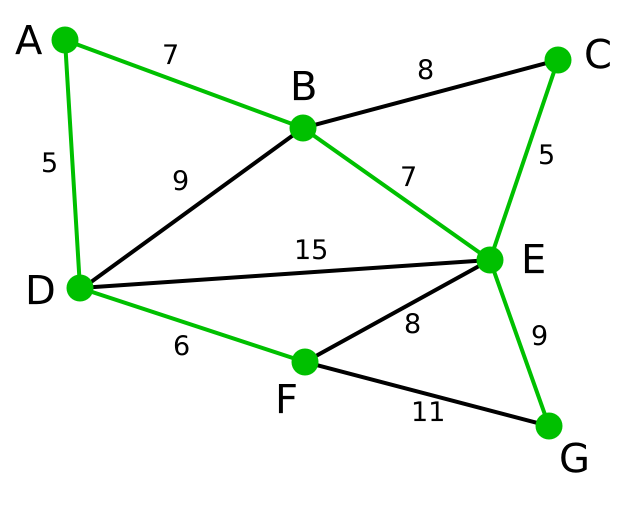
解决最小生成树(Minimum spanning tree)问题的算法,书上介绍了两个:Prime算法和Kruskal算法。
Prim算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <stdio.h>
#include "graph.h"
extern void DispMat1(MGraph);
void Prim(MGraph g, int v)
{
int lowcost[MAXV], min, n = g.n;
int closest[MAXV], i, j, k;
for (i = 0; i < n; i++)
{
lowcost[i] = g.edges[v][i];
closest[i] = v;
}
for (i = 1; i < n; i++) // 找出n - 1个顶点
{
min = INF;
for (j = 0; j < n; j++)
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
k = j;
}
}
printf(" 边(%d, %d)权为:%d\n", closest[k], k, min);
lowcost[k] = 0; // 标记k已经加入U
for (j = 0; j < n; j++)
{
if (g.edges[k][j] != 0 && g.edges[k][j] < lowcost[j])
{
lowcost[j] = g.edges[k][j];
lowcost[j] = k;
}
}
}
}
|
Kruskal算法
实现克鲁斯卡尔算法的关键是判断选取的边是否与生成树中已保留的边形成回路,这可以通过判断边的两个顶点所在的连通分量来解决(给顶点所在连通分量编号)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| typedef struct
{
int u; // 边的起始顶点
int v; // 边的终止顶点
int w; // 边的权值
} Edge;
void Kruskal(MGraph g, int v)
{
int i, j, u1, v1, sn1, sn2, k;
int vset[MAXV]; // 存放所有边
Edge E[MaxSize]; // e数组的下标从0开始计
k = 0;
for (i = 0; i < g.n; i++) // 由g产生的边集E
{
for (j = 0; j < g.n; j++)
{
if (g.edges[i][j] != 0 && g.edges[i][j] != INF)
{
E[k].u = i;
E[k].v = i;
E[k].w = g.edges[i][j];
k++;
}
}
}
InsertSort(E, g.e);
for (i = 0; i < g.n; i++)
{
vset[i] = i;
}
k = 1; // k表示当前构造生成树的第几条边,初值为1
j = 0; // E中边的下标,初值为0
while (k < g.n)
{
u1 = E[j].u;
v1 = E[j].v;
sn1 = vset[u1];
sn2 = vset[v1];
if (sn1 != sn2)
{
printf(" (%d, %d): %d\n", u1, v1, E[j].w);
k++; // 生成边数增1
for (i = 0; i < g.n; i++) // 两个集合统一编号
{
if (vset[i] == sn2) // 集合编号为sn2的改为sn1
{
if (vset[i] == sn2)
{
vset[i] = sn1;
}
}
}
}
j++;
}
}
|
算法参考: